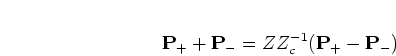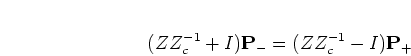Back to Kemp Acoustics Home



Next: Multimodal reflectance of a
Up: Multimodal reflections
Previous: Introduction
Contents
A formula relating the forward and backward components of the
volume velocity amplitude vector in terms of the impedance matrix
was quoted in Pagneux et al. [32] p.2046. Here we show the
derivation for the pressure amplitude vector. The first step is to express
the total pressure amplitude vector  as the sum of the forward
going (
as the sum of the forward
going (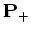 ) and backward going (
) and backward going (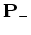 ) components:
) components:
 |
(6.1) |
Now the total volume velocity is expressed using the same notation for forward
and backward components:
 |
(6.2) |
Recalling the characteristic impedance of higher modes from equation
(2.36), the ratio of the 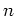 th element in
the forward going pressure vector to the
th element in
the forward going pressure vector to the 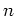 th element in the forward
going volume velocity vector is
th element in the forward
going volume velocity vector is
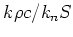 .
Using
.
Using 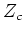 , the diagonal characteristic
impedance matrix defined in equation (2.42):
, the diagonal characteristic
impedance matrix defined in equation (2.42):
 |
(6.3) |
Similarly for the backward going waves,
 |
(6.4) |
Defining the impedance
matrix at a particular point as 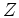 with
with
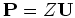 we get
we get
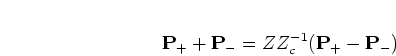 |
(6.5) |
which may be rearranged to give
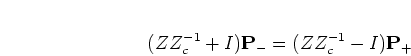 |
(6.6) |
so the result is
 |
(6.7) |
where 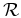 is the reflectance matrix:
is the reflectance matrix:
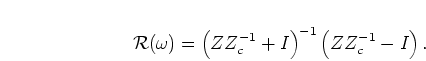 |
(6.8) |
Notice that this is a correction to the reflectance matrix
quoted in [41]. The correction arises because
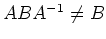 in general, even when
in general, even when 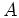 is a diagonal matrix. The correction only has an
effect on the non-diagonal entries in
is a diagonal matrix. The correction only has an
effect on the non-diagonal entries in 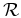 . The graphs presented in
[41] are of the
. The graphs presented in
[41] are of the
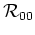 element and are unaffected by
the correction.
element and are unaffected by
the correction.
Back to Kemp Acoustics Home



Next: Multimodal reflectance of a
Up: Multimodal reflections
Previous: Introduction
Contents
Jonathan Kemp
2003-03-24
![]() as the sum of the forward
going (
as the sum of the forward
going (![]() ) and backward going (
) and backward going (![]() ) components:
) components: