Back to Kemp Acoustics Home



Next: Bibliography
Up: thesis
Previous: Projection matrix in cylindrical
Contents
Inductance method
The inductance method due to Kergomard and Garcia [57] is reviewed
here. The multimodal method was treated and the results used
to get a polynomial for the frequency dependent inductance, 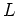 ,
so that the formula
,
so that the formula
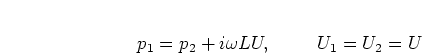 |
(C.1) |
matches the multimodal treatment when
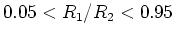 and
and
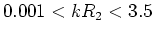 .
Here
.
Here 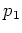 is the pressure immediately to the left of the discontinuity and
is the pressure immediately to the left of the discontinuity and
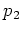 is the pressure immediately to the right of the discontinuity.
is the pressure immediately to the right of the discontinuity.
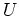 is the volume velocity, matched on both sides as with the plane wave
approximation. The pressures and volume velocity are scalars here, not
vectors since the multimodal effects are represented by the inductance.
is the volume velocity, matched on both sides as with the plane wave
approximation. The pressures and volume velocity are scalars here, not
vectors since the multimodal effects are represented by the inductance.
Now we will work out the reflectance for a plane wave incident on a
discontinuity between two infinite cylinders. We do this by expressing both
the equations in (C.1) in terms of forward and backward
going waves and solving. The pressure on
the left is the sum of incident and reflected waves:
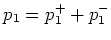 . The pressure on the right is simply the transmitted
term
. The pressure on the right is simply the transmitted
term 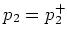 .
.
The volume velocity on the left is then
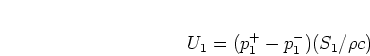 |
(C.2) |
while on the right the volume velocity is
 |
(C.3) |
From equation (C.1) the volume velocity is the same on
each side of the discontinuity for this method giving:
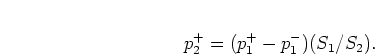 |
(C.4) |
Now we turn to the first part of equation (C.1).
Substituting in the pressure as the sum of the forward and backward going waves
and putting
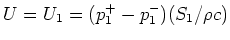 gives
gives
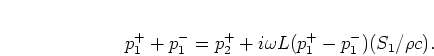 |
(C.5) |
In order to work out the reflectance we need to remove 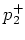 to obtain
an expression featuring only
to obtain
an expression featuring only 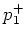 and
and 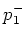 . We therefore
substitute
. We therefore
substitute 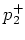 from equation (
from equation (![[*]](file:/usr/local/share/lib/latex2html/icons/crossref.png) ) into
equation (C.5).
) into
equation (C.5).
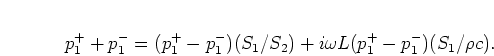 |
(C.6) |
Rearranging we get the reflection coefficient, the ratio of the reflected and
incident waves:
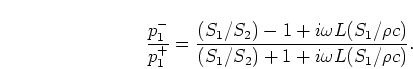 |
(C.7) |
As with the multimodal method this may be expressed in terms of dimensionless
variables 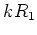 and
and
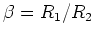 ;
;
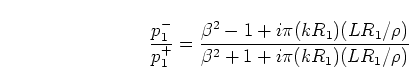 |
(C.8) |
where 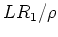 is a function of the dimensionless variables and is
tabulated in table 2 (A) of [57].
This formula is used to calculate the inductance method reflectance shown in
figure 6.1 of section 6.4.
is a function of the dimensionless variables and is
tabulated in table 2 (A) of [57].
This formula is used to calculate the inductance method reflectance shown in
figure 6.1 of section 6.4.
Back to Kemp Acoustics Home



Next: Bibliography
Up: thesis
Previous: Projection matrix in cylindrical
Contents
Jonathan Kemp
2003-03-24
![]() ,
so that the formula
,
so that the formula
![]() . The pressure on the right is simply the transmitted
term
. The pressure on the right is simply the transmitted
term ![]() .
.