Back to Kemp Acoustics Home



Next: Inductance method
Up: Projection at a discontinuity
Previous: Volume velocity
Contents
In polar coordinates equation (B.6) becomes
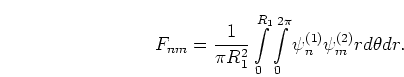 |
(B.15) |
Substituting in equation (2.48) for 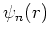 and
performing the integration with respect to
and
performing the integration with respect to 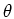 gives:
gives:
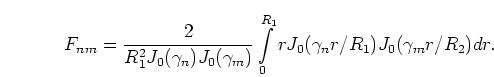 |
(B.16) |
This is in the form of the standard integral from
equation (A.1) of appendix A. Substituting in
the variables: 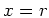 ,
, 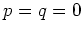 ,
,
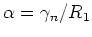 and
and
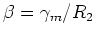 gives
gives
When the evaluation is carried out the contribution when 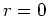 is zero giving:
is zero giving:
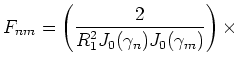 |
| |
|
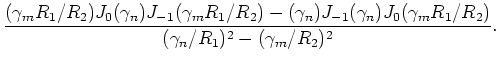 |
(B.17) |
Now noticing from equation (A.2) that
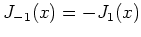 and using the fact that
and using the fact that 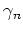 is a zero of
is a zero of
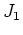 the second term vanishes:
the second term vanishes:
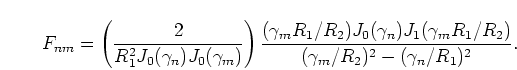 |
(B.18) |
Expressing this in terms of the ratio of the radii,
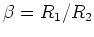 we
get
we
get
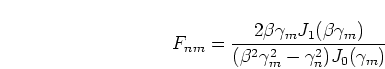 |
(B.19) |
hence we have proved equation (2.85).
The integration used to obtain the analytical expression for 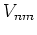 is
identical to that for
is
identical to that for 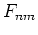 except that the labels are interchanged for
surface 1 and surface 2. Interchanging
except that the labels are interchanged for
surface 1 and surface 2. Interchanging 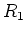 and
and 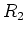 means that
means that
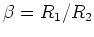 will be replaced with
will be replaced with
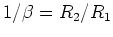 giving
giving
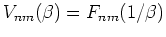 .
.
Back to Kemp Acoustics Home



Next: Inductance method
Up: Projection at a discontinuity
Previous: Volume velocity
Contents
Jonathan Kemp
2003-03-24
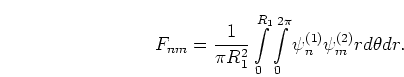
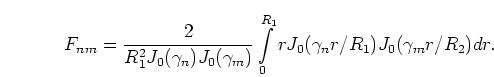
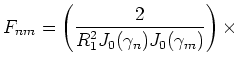
![$\displaystyle \left[
\frac{(\gamma_m r/R_2) J_0(\gamma_n r/R_1) J_{-1}(\gamma_m...
...0(\gamma_m r/R_2)}
{(\gamma_n/R_1)^2 - (\gamma_m/R_2)^2}
\right]_{r=0}^{r=R_1}.$](img788.png)
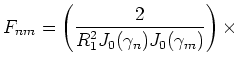
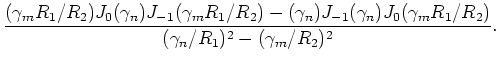
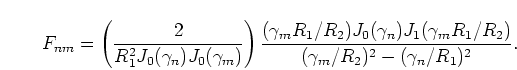
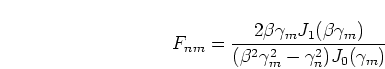
![]() is
identical to that for
is
identical to that for ![]() except that the labels are interchanged for
surface 1 and surface 2. Interchanging
except that the labels are interchanged for
surface 1 and surface 2. Interchanging ![]() and
and ![]() means that
means that
![]() will be replaced with
will be replaced with
![]() giving
giving
![]() .
.