Back to Kemp Acoustics Home



Next: Volume velocity
Up: General expression
Previous: General expression
Contents
We denote the pressure field on surface 1 as 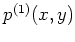 and the pressure
field on surface 2 as
and the pressure
field on surface 2 as 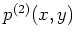 . In plane wave
propagation we saw that the pressure is taken to be the same on both sides of
the discontinuity. In the multimodal case the pressure field is matched
at either side. For the case shown where
. In plane wave
propagation we saw that the pressure is taken to be the same on both sides of
the discontinuity. In the multimodal case the pressure field is matched
at either side. For the case shown where 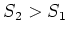 the
pressure is matched on the air they share,
the
pressure is matched on the air they share, 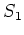 .
.
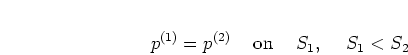 |
(B.1) |
Now the concept of orthogonality of the modes is used.
Recalling our orthogonality relation from equation
(2.47):
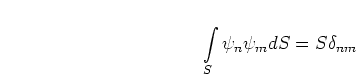 |
(B.2) |
it follows that the integration of the mode profile 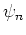 with a general
pressure field,
with a general
pressure field, 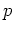 will extract the component of the
will extract the component of the 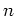 th mode in the pressure
field. Using the fact that the pressure may be expressed as a sum of
the modes from equation 2.26
(ignoring the
th mode in the pressure
field. Using the fact that the pressure may be expressed as a sum of
the modes from equation 2.26
(ignoring the
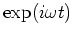 time factor):
time factor):
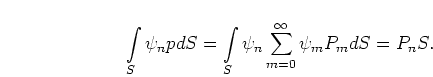 |
(B.3) |
We will use 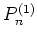 and
and 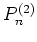 to denote the complex mode
amplitudes on surfaces 1 and 2 respectively.
to denote the complex mode
amplitudes on surfaces 1 and 2 respectively. 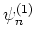 and
and
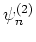 are the corresponding mode profiles on surfaces 1 and 2.
Combining equations (B.1) and
B.3) gives
are the corresponding mode profiles on surfaces 1 and 2.
Combining equations (B.1) and
B.3) gives
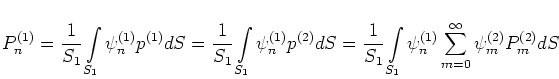 |
(B.4) |
which may be written as
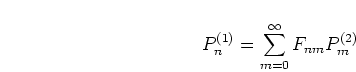 |
(B.5) |
where
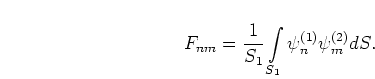 |
(B.6) |
Using matrix notation,
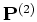 is a column vector whose entries are
given by
is a column vector whose entries are
given by 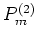 and
and
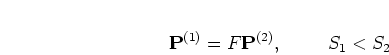 |
(B.7) |
where F is a matrix with elements 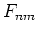 . We have now proved
equations (2.79) and (2.80) from chapter 2.
. We have now proved
equations (2.79) and (2.80) from chapter 2.
We now have a formula giving the pressure on a smaller cross-section
at a discontinuity from the pressure on a larger cross-section on the other
side. Since 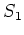 and
and 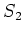 are assumed to not be separated by any distance
along the
are assumed to not be separated by any distance
along the 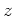 axis the formula holds whatever side the largest cross-section
is on. Consider if
axis the formula holds whatever side the largest cross-section
is on. Consider if 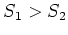 . Now section 1 is the larger cross-section
meaning that we just have to interchange the labels 1 and 2 in
equation (B.7):
. Now section 1 is the larger cross-section
meaning that we just have to interchange the labels 1 and 2 in
equation (B.7):
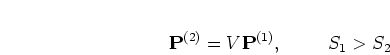 |
(B.8) |
where 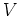 is a matrix with the elements defined by
is a matrix with the elements defined by
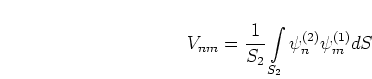 |
(B.9) |
Back to Kemp Acoustics Home



Next: Volume velocity
Up: General expression
Previous: General expression
Contents
Jonathan Kemp
2003-03-24
![]() and the pressure
field on surface 2 as
and the pressure
field on surface 2 as ![]() . In plane wave
propagation we saw that the pressure is taken to be the same on both sides of
the discontinuity. In the multimodal case the pressure field is matched
at either side. For the case shown where
. In plane wave
propagation we saw that the pressure is taken to be the same on both sides of
the discontinuity. In the multimodal case the pressure field is matched
at either side. For the case shown where ![]() the
pressure is matched on the air they share,
the
pressure is matched on the air they share, ![]() .
.
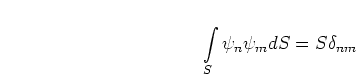
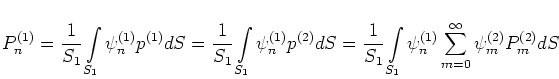
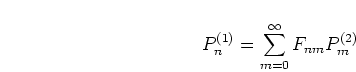
![]() and
and ![]() are assumed to not be separated by any distance
along the
are assumed to not be separated by any distance
along the ![]() axis the formula holds whatever side the largest cross-section
is on. Consider if
axis the formula holds whatever side the largest cross-section
is on. Consider if ![]() . Now section 1 is the larger cross-section
meaning that we just have to interchange the labels 1 and 2 in
equation (B.7):
. Now section 1 is the larger cross-section
meaning that we just have to interchange the labels 1 and 2 in
equation (B.7):